[QPE] 有 QFT 的 QPE

2023 iThome 鐵人賽

DAY 2

自我挑戰組

不嚴謹的量子計算雜談系列第 2 篇

15th鐵人賽量子計算

bwl

2023-09-11 08:34:47

562 瀏覽

分享至

今天要介紹第一個系列：Quantum Phase Estimation (QPE)，的第一個演算法：QPE with QFT (Quantum Fourier Transformation，量子傅立葉轉換)。這裡對於 QFT 不會詳加介紹，有興趣的讀者可以參考第一天的學習資源 (尤其是 QCQI 的第五章)。由於這是 QPE 系列的第一篇，我們先看看什麼是 QPE 以及為什麼 QPE 很重要。

我們知道，量子態 (quantum state) 的演化 (evolution) 經由么正算子 (unitary operator；這裡我們將 operator 和 matrix 視為同一概念，因此以下將以 unitary matrix 稱之) 進行。令 $U$ 為我們感興趣的 unitary matrix，而 $|u\rangle$ 為 $U$ 的一個特徵向量 (eigenvector)，滿足：

$U|u\rangle = \exp(2\pi i\theta)|u\rangle.$

( $|u\rangle$ 是稱為 ket 的量子態表示法，細節請參考 QCQI。) QPE 的目標就是獲得實數 $\theta$ 的資訊！( $U$ 、 $|u\rangle$ 和 $\theta$ 的定義沿用至下兩篇文章。)

為什麼我們對 QPE 感興趣？舉例來說，著名的 Shor's factoring 演算法和 HHL 演算法都用到了 QPE 演算法作為 subroutine！(夠重要了吧？)

QPE with QFT 應該是最常見的一種 phase estimation 演算法，它的概念非常優雅簡潔，主要分成四階段：(如附圖；圖來源：QCQI, p. 223)

準備 uniform superposition
使用 controlled- $U^{j}$
逆量子傅立葉轉換 (= Inverse QFT = IQFT)
測量

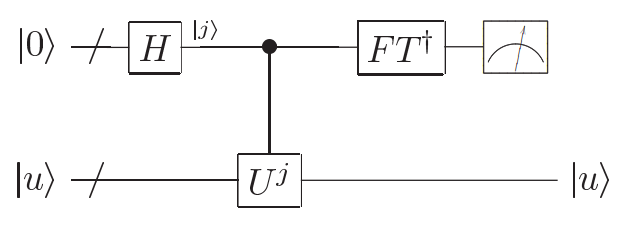
從上圖我們看到，這個系統的量子暫存器 (quantum register) 分為兩部分：上半部的 $|0\rangle$ ，用來儲存 phase $\theta$ ( $|0\rangle = |0^{\otimes d}\rangle$ ， $d$ 是 $\theta$ 的精確度；本演算法使 $|0\rangle \to |\tilde{\theta}\rangle$ )，有人將此暫存器稱為 clock register；下半部的 $|u\rangle$ 用來儲存特徵向量。

雖然 QPE with QFT 在演算法層面很簡潔，而且非常實用 (三種演算法中，唯一可以直接估計疊加態的 phase)，但是在當前的 (2023 年) 的量子電腦上難以實現：因為相應的量子電路的深度太大 (深度 = 最大串聯量子閘數；深度大導致量子閘的錯誤不斷累積)，而且所需要的量子位元 (qubit) 會隨著精確度的要求而增長！明天要介紹的 Iterative QPE 正有著減小深度及 qubit 的優勢。敬請期待！